Propositional Logic

It is important to think about the kind of meanings and concepts connected with words. We have seen that there is an incredible amount of complex information connected with words.

However, we do not communicate just by using single words. We speak and write in sentences. That is even more complicated.

Just thinking about all the complicated information flying around in one sentence could drive you crazy! How does Semantics deal with that? Well, first of all, by simplifying everything.

In Propositional Logic, we treat sentences as propositions.
In Propositional Logic, truth values are assigned to propositions (sentences). Truth values are either True(T) or False (F). Look at the two following sentences:
(1) Ken hit Jim.
(2) Jim was hit by Ken.
Clearly, these are two different sentences. However, Propositional Logic claims that these different sentences may be converted into identical propositions.

Propositional logic labels propositions, usually starting with the small letter p. If you have two propositions, they are labelled p and q, and so on.

Propositions have truth values. So we can ask, under what conditions is a proposition p true (T) or false (F)? Say we have a proposition p such as the following:
p = Ben is studying.
Then we can say that p = T when Ben is studying and p = F when he is not.

Of course, there are always problems related to truth values. Can you really be sure he is studying? What if the person who says he is studying is not reliable? However, we imagine a simple world in which we can say straightforwardly whether or not propositions like this are true or false.

So, say we add another proposition q to p:
p = Ben is studying.
q = Ben is sleeping.
We can say that p = F if q = T. Do you agree? If Ben is sleeping, he is not studying, right?

Say we add another proposition r to p and q:
p = Ben is studying.
q = Ben is sleeping.
r = Ben is using his mobile phone.
What happens to p and q if r = T? We can say that p is only true if q is false. Can we say that p is only true if r is false? Can we say that q is only true if p and r are both false? Think about it, but try not to get a headache!

Now simple propositions like this can be turned into complex propositions by using Logical Constants or connectives.

There are a number of ways to write these, but you can get the basic idea from the following:
Conjunction ∧ (or &) means “and”
Disjunction ∨ means “or”
Implication → means ” if … then”
Negation ¬ means “not”
Equivalence ≡ means “if and only if (iff)”
Say we have a proposition such as (3) below:
(3) p ∧ q
When is (3) true? Propositional Logic makes use of so-called truth tables to determine whether a proposition is true or not.

Here is a truth table for the disjunction:

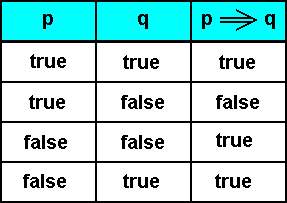
Here’s a truth table for implication:
Here’s a truth table for negation which can be written as ~ or – as well as ¬ so try not to get confused!:

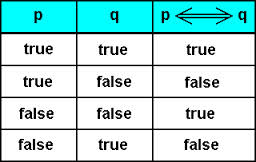
Here’s a truth table for equivalence, which can be written as ≡ or ⇔.