Predicate Logic

Propositional Logic treats simple propositions as having no internal structure. Predicate Logic is used to help us think about the internal structure of simple propositions and how to represent sentence meaning.
Say we have a sentence such as p:
p = John loves Mary
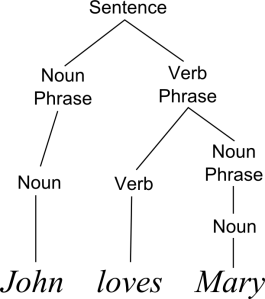
In Predicate Logic, this relationship is labelled like this:
Love (x, y)
x = John
y = Mary
Love (john, mary)
This gives us a simple, formal way of defining the proposition as a “predication.”
Predications consist of a Predicate (Capital Letter) and a set of arguments (small letter):
Predicate (arg1, …, argN)
One way of doing this is as follows:
P (x) means “x is a P”
For example, we could say “Japan is a country” like this:

Country (japan)
This is a so-called one-place predicate.
A two-place predicate has two arguments.
For example, we could say that “John loves Mary” like this:
Loves (john, mary)
The Predicate is Love and the arguments are john and mary.
You could also have a three-place predicate. For example, we could say “John sends Mary his love” like this:
Send (john, mary, love)
Predications can also involve quantifiers. This allows us to think about the relations between sets of things. For example, think about these two sets — the set of crazy people and the set of linguists.
The set of linguists: A
The set of crazy people: B
Perhaps we want to say that “All linguists are crazy.”
The word “all” indicates that one set is included in the other. In this case the set of linguists A is completely included in the set of crazy people B. There are no linguists who are not crazy. If you are a linguist, you are crazy.
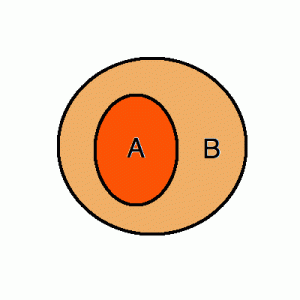
This is how it is represented in Predicate Logic:
∀x (Linguist (x) → Crazy (x))
The upside-down A means “for all” and it allows us to look at everything that is x and check them off against the sets of linguists and crazy people. In this formula, we are saying that for every individual x that is in the set of linguists, that individual is also in the set of crazy people. Of course, we hope this proposition is false!
Here is another example. Perhaps we want to say “All men love Mary.” We could do it like this:
∀x (Man (x) → Love (x, mary))
Now maybe only some men love Mary and only some linguists are crazy. How do we represent that in Predicate Logic?
Some linguists are crazy = ∃x (Linguist (x) & Crazy (x))
The backward E indicates that two sets intersect.
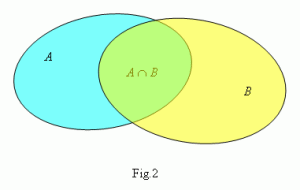
For the set of individuals x, there will be at least one individual who is both in the set of linguists and in the set of crazy people.
Or perhaps we want to say “A girl lives in Tsuru.” We could do it like this:
∃x (Girl (x) & Lives_in (x, tsuru))
Or perhaps we want to say “No students like Predicate Logic.” We could do it like this:
¬∃x (Student (x) & Like (x, predicate_logic))
In this case the sets do not intersect at all. It is not the case that there is at least one individual who is both in the set of students and in the set of individuals who like Predicate Logic.
Predicate Logic allows us to analyze the internal structure of propositions and give a detailed formal representation of sentence meaning.
